实验目的 |
1、加深对轮廓拟合概念的理解;
2、掌握常用的轮廓拟合方法和编程方法;
|
实验原理 |
图像轮廓是指在数字图像中其周围像素灰度有阶跃变化或屋顶变化的那些像素的集合。轮廓是一组边缘点的集合,可以理解为将一系列边缘点连接起来而形成的目标与背景的分界。
根据轮廓的特征,可以分为封闭轮廓和间断轮廓。封闭轮廓是指一个完整区域的连续边界,例如一个圆或三角形轮廓。由此可以将整个区域划分为三个部分,即边界、内部和外部。间断轮廓是指一部分区域的边界,例如直线边缘的一部分或者圆弧。间断轮廓也可能使完整的封闭轮廓在不理想条件下导致的部分轮廓缺失,例如对比度太弱、边缘检测阈值设置太高等原因所致。
通常的图像轮廓具有规则的数学模型,例如线段(直线边缘)、二次曲线(圆、圆弧、渐开线边缘)、三次样条曲线等。
提取凸显轮廓一般需要如下过程:
(1) 图像滤波:去除图像噪声,平滑化;
(2) 边缘检测:确定边缘点位置;
(3) 图像修补:需要通过平滑、形态学等方法,去除噪声点、毛刺、空洞等;
(4) 图像细化:去除简单边缘点,获得边缘脊;
(5) 边界跟踪:将边缘点连接起来,获得物体的轮廓边界;
(6) 边缘拟合:计算规则边缘位置(直线、曲线)。
图像细化是将边缘的宽度降为单个像素的宽度。图像细化的原则是:保持连通性(连续性)且不减小形状长度的条件下,消去区域中那些不是端点的简单边界点,降低人为因素所造成的影响。
边界跟踪的过程,是由图像梯度出发,依次搜索并连接相邻边缘点,从而逐步检测出边界。目的是要求目标轮廓边界细、连续无间断、准确。
轮廓曲线拟合,是通过已知的多个边界点坐标,获取整体轮廓位置信息。拟合的作用,一是确定整体轮廓位置信息;二是利用误差平均效应,减小个别边缘点的误差对整体轮廓的影响,显著提供定位精度。
直形边缘是涉及最多的规则轮廓,例如刻线、大曲率半径的曲线近似,许多轮廓可以看作多端直线的组合。直线拟合方法有鲁棒回归法和最小二乘法。最小二乘法的依据是使得残差平方和最小,即所有点到回归直线的距离的平方和最小。最小二乘拟合直线通过所有边缘点的平均点,但残余误差平方和最小。对于噪声呈正态分布的情形,最小二乘法是最佳拟合方法;对于噪声非正态分布分布,最小二乘法是非最佳拟合方法,但是近似最佳拟合方法。
对于一组测量数据点 ,最小二乘直线边缘表达式为: ,最小二乘直线边缘表达式为:
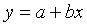
其中的系数分别为:
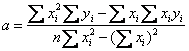 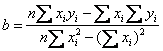
圆和圆弧是最为常见的二次曲线轮廓,其中圆度误差也是机械零部件的一项重要参数,因此经常会涉及到。
对于一组测量数据点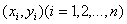 ,最小二乘圆的表达式为: ,最小二乘圆的表达式为:
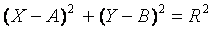
令: 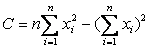
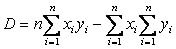
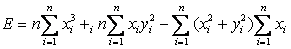
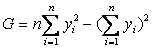
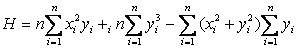
可有: 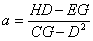 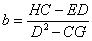

最后得:  
|
实验仪器与设备 |
(1) 黑白数字摄像机:同前;
(2) FA镜头:同前;
(3) LED光源:同前;
(3) 视觉检测实验台:同前;
(4) 被测试件:;
(5) 计算机:同前,包括大恒数字摄像机应用接口库。
|
实验内容与过程 |
(1) 打开计算机电源,运行计算机桌面上的摄像机演示程序demo,检查是否可以捕获黑白图像。
(2)调整光源、被测物、镜头、数字摄像机,保证清晰成像,并使得被测轮廓占据约半个视场,且位置居中为宜。利用VC语言采集一幅图像,并保存图像。
(3) 编制VC语言程序,实现直线轮廓的最小二乘拟合,并对两个直线轮廓分别进行拟合,保存拟合结果。观察实际轮廓与拟合结果的差异程度。
(4) 编制VC语言程序,实现圆轮廓的最小二乘拟合,并对具体的两个圆轮廓进行拟合,保存拟合结果。观察实际轮廓与拟合结果的差异程度。
|
实验报告 |
将实验中保存的图像分别拷贝出来,放入下面的相应表格中,并将总结的现象和规律填入表格。
原始图像 |
内容 |
采集图象 |
结果 |
|
现象 |
|
直线轮廓拟合 |
序号 |
第一次 |
第二次 |
轮廓 |
直线1 |
直线2 |
拟合
结果 |
|
|
现象 |
|
|
规律 |
|
圆轮廓拟合 |
序号 |
第一次 |
第二次 |
轮廓 |
圆1 |
圆2 |
拟合
结果 |
|
|
现象 |
|
|
规律 |
|
|