实验原理 |
边缘检测是图像分割、目标区域的识别、区域形状提取等图像分析领域十分重要的基础，是图像识别中提取图像特征的一个重要属性，图像理解和分析的第一步往往就是边缘检测，目前它以成为机器视觉研究领域最活跃的课题之一，在工程应用中占有十分重要的地位。
物体的边缘是以图像的局部特征不连续的形式出现的，也就是指图像局部亮度变化最显著的部分，例如灰度值的突变、颜色的突变、纹理结构的突变等，同时物体的边缘也是不同区域的分界处。图像边缘有方向和幅度两个特性，通常沿边缘的走向灰度变化平缓，垂直于边缘走向的像素灰度变换剧烈，根据灰度变化的特点，可分为阶跃型、房顶型和凸缘型，如图所示，这些变化对应图像中不同的景物。
由于边缘是图像上灰度变化最剧烈的地方，因此边缘检测就是利用了这个特点，对图像各个像素点进行微分或求二阶微分来确定边缘像素点。一阶微分图像的峰值处对应着图像的边缘点；二阶微分图像的过零点处对应着图像的边缘点。根据数字图像的特点，处理图像过程中常采用差分来代替导数运算，对于图像的简单一阶导数运算，由于具有固定的方向性，只能检测特定方向的边缘，所以不具有普遍性。为了克服一阶导数的缺点，我们定义了图像的梯度为梯度算子：
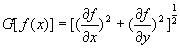
它是图像处理中最常用的一阶微分算法，式子中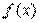 表示图像的灰度值，图像梯度的最重要性质是梯度的方向是在图像灰度最大变化率上，它恰好可以放映出图像边缘上的灰度变化。
图像边缘提取的常用梯度算子有Robert算子、Sobel算子、Prewitt算子、Krisch算子等，其中Sobel算子应用较为广泛。Sobel算子定义如下：对数字图像{f(i,j)}的每个像素，考察它上、下、左、右邻点灰度的加权差，与之接近的邻点的权大。Sobel算子为：
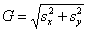
以3*3模板为例，邻域内各像素点的位置关系如下：
| f(i-1,j-1) |
f(i-1,j) |
f(i-1,j+1) |
f(i,j-1) |
f(i,j) |
f(i,j+1) |
f(i+1,j-1) |
f(i+1,j) |
f(i+1,j+1) |
Sx为：
Sy为：
Sobel梯度算子是先做成加权平均，再微分，然后求梯度，即：
△x=f(x-1,y+1)+2f(x,y+1)+f(x+1,y+1)-f(x-1,y-1)-2f(x,y-1)-f(x+1,y-1)
△y=f(x-1,y-1)+2f(x-1,y)+f(x-1,y+1)-f(x+1,y-1)-2f(x+1,y)-f(x+1,y+1)
G[f(x,y)]=|△x|+|△y|
二阶微分算子主要有Laplacian算子、LoG算子、Canny算子等。拉普拉斯的算子是不依赖于边缘方向的二阶微分算子，它是一个标量而不是向量，具有旋转不变,既各向同性的性质。对于数字图像来说，拉普拉斯算子可以简单表示为：
G[i,j]=|f[i+1,j]+f[i-1,j]+f(i,j+1)+f[i,j-1]-4f[i,j]|;
对于3*3模板，拉普拉斯算子可表示为：
|
